The Rayleigh Quotient

Original Post - 06 Jun 2021 - Michael H. Scott

Visit Structural Analysis Is Simple on Substack.

Eigenvalue analysis wasn’t giving me what I wanted the other day. So, to make a long story short, I decided to try Rayleigh’s method.

I won’t go through all the details of Rayleigh’s method, but the basic idea is you can obtain a very good approximation of the fundamental frequency of a structural model by using the displacements due to a static analysis as the shape function in Rayleigh’s quotient.

This makes sense–the eigenvalue equation, \({\bf K}{\bf x}=\omega^2{\bf M}{\bf x}\), is one of static equilibrium.

After some manipulation (see Chapter 8 of the Chopra book, 5th ed.), Rayleigh’s quotient can be expressed as

\[{\displaystyle \omega^2 = \frac{g \sum m_j u_j}{\sum m_j u_j^2}}\]

where u_j is the displacement at the j^th degree-of-freedom (DOF) due to static loads in direct proportion to the mass at the DOF, i.e., a load pattern where F_j=m_jg at each DOF in the direction of vibration.

Implementing Rayleigh’s method in OpenSees is pretty straightforward. I’ll show the method with Example 8.9, a five story shear frame from the Chopra book.

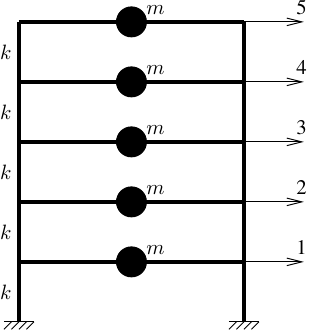
Five story shear frame

There’s a few ways to define shear frame models. My favorite approach is to use a one-dimensional model with zero length springs in series.

N = 5 # Number of stories
k = 110 # Story stiffness
m = 1.25 # Floor mass

g = 386.4

ops.wipe()
ops.model('basic','-ndm',1,'-ndf',1)

ops.uniaxialMaterial('Elastic',1,k)

ops.node(0,0); ops.fix(0,1)
for j in range(N):
    ops.node(j+1,0)
    ops.mass(j+1,m)
    ops.element('zeroLength',j+1,j,j+1,'-mat',1,'-dir',1)

The code to define a load pattern and compute the Rayleigh quotient is easy for the common case where mass is lumped at the nodes.

ops.timeSeries('Constant',1)
ops.pattern('Plain',1,1)
for j in range(N):
    mj = ops.nodeMass(j+1,1)
    ops.load(j+1,mj*g)
    
ops.analysis('Static')
ops.analyze(1)

num = 0; den = 0
for j in range(N):
    mj = ops.nodeMass(j+1,1)
    uj = ops.nodeDisp(j+1,1)
    num += mj*uj
    den += mj*uj*uj
    
w2 = g*num/den
print(f'Rayleigh: w2 = {w2}, Period = {2*3.14159/w2**0.5}')
w2 = ops.eigen(1)[0]
print(f'Eigenanalysis: w2 = {w2}, Period = {2*3.14159/w2**0.5}')

For models with more than one DOF per node, the code to compute the Rayleigh quotient is similar to what’s shown for modal participation factors.

Here are the results for this simple model.

Periods from Rayleigh quotient and eigenvalue analysis

The period is pretty long for a five story frame; however, sometimes a number is a number.

OpenSees Cloud

OpenSees AMI

The Rayleigh Quotient