OpenSees Cloud

OpenSees AMI

Multiple-Support Excitation

Original Post - 29 Aug 2021 - Michael H. Scott

Visit Structural Analysis Is Simple on Substack.

Structural systems typically have different ground accelerations at supports separated by long distances. These systems can be a single structure such as a long span bridge or multiple structures in a region.

While most OpenSees analyses use uniform excitation with effective earthquake forces applied to the dynamic DOFs of the model, the framework also accommodates multi-support excitation. The basic idea is that the locations of support excitation become DOFs where the ground displacement is input–much like putting sp constraints inside a load pattern.

For more details on the equation of motion for multiple-support excitation, see Ch. 9 of Chopra, 5th edition. Although Chopra presents the equation of motion for linear-elastic models, the extension to nonlinear models is straightforward.

But rather than get into details of the equation of motion, I’d like to show how to apply multiple-support excitation in OpenSees. As usual, so we don’t get mired in the details of specific element and material models, I’ll use a simple 1D model.

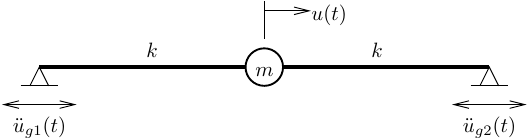
After defining the model, we define time series for two ground motions, then impose the ground motions at the two supports.

import openseespy.opensees as ops

k = 60
m = 2
g = 386.4

ops.wipe()
ops.model('basic','-ndm',1,'-ndf',1)

ops.node(1,0); ops.fix(1,1)
ops.node(2,0); ops.mass(2,m)
ops.node(3,0); ops.fix(3,1)

ops.uniaxialMaterial('Elastic',1,k)

ops.element('zeroLength',1,1,2,'-mat',1,'-dir',1)
ops.element('zeroLength',2,2,3,'-mat',1,'-dir',1)

ops.timeSeries('Path',1,'-dt',0.02,'-filePath','tabasFN.txt','-factor',g)
ops.timeSeries('Path',2,'-dt',0.02,'-filePath','tabasFP.txt','-factor',g)

ops.pattern('MultipleSupport',1)
ops.groundMotion(1,'Plain','-accel',1)
ops.imposedMotion(1,1,1) # node, dof, gmTag
ops.groundMotion(2,'Plain','-accel',2)
ops.imposedMotion(3,1,2)

ops.constraints('Transformation')

The default integration for obtaining ground velocity and displacement from ground acceleration is the trapezoidal rule. You can also use Simpson’s rule. And since you’ll be imposing non-homogeneous boundary conditions, you will need to use the Transformation constraint handler.

In addition, the groundMotion and imposedMotion objects must be defined after the load pattern. In Tcl speak, these objects should be inside braces.

timeSeries Path 1 -dt 0.02 -filePath tabasFN.txt -factor $g
timeSeries Path 2 -dt 0.02 -filePath tabasFP.txt -factor $g

pattern MultipleSupport 1 {
   groundMotion 1 Plain -accel 1
   imposedMotion 1 1 1 ;# node, dof, gmTag
   groundMotion 2 Plain -accel 2
   imposedMotion 3 1 2
}

constraints Transformation

After performing dynamic analysis, the displacement response histories of the mass and the two supports are shown below.

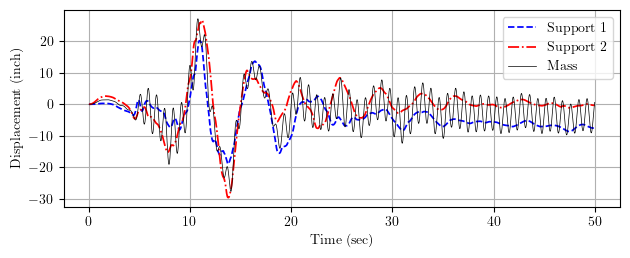
We see that the supports have different displacement response histories, as expected, while the dynamic DOF vibrates. Multiple-support excitation is fairly straightforward in OpenSees.

–

The remainder of this post deals with two ways to apply uniform excitation to the simple 1D model. First, we can impose the same ground motion at the supports.

ops.timeSeries('Path',1,'-dt',0.02,'-filePath','tabasFN.txt','-factor',g)

ops.pattern('MultipleSupport',1)
ops.groundMotion(1,'Plain','-accel',1)
ops.imposedMotion(1,1,1) # node, dof, gmTag
ops.imposedMotion(3,1,1)

ops.constraints('Transformation')

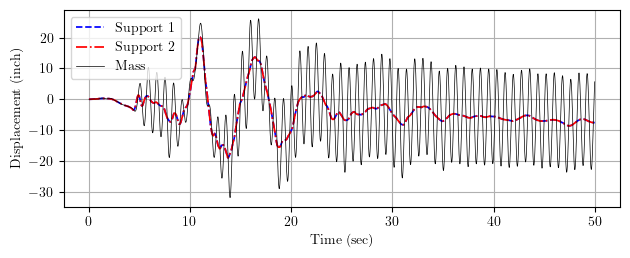
Alternatively, we can apply a standard uniform excitation. No constraint handler required.

ops.timeSeries('Path',1,'-dt',0.02,'-filePath','tabasFN.txt','-factor',g)

ops.pattern('UniformExcitation',1,1,'-accel',1) # tag, dir, tsTag

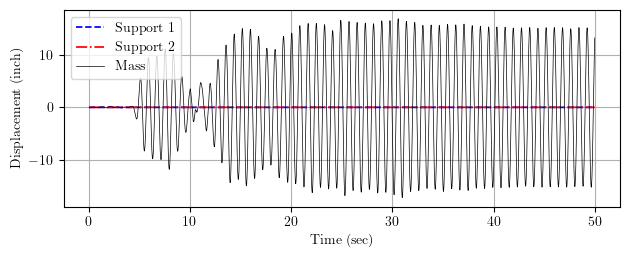
These two approaches give the same response for the dynamic DOF (relative to the ground displacement). But of course we lose the ground displacement when doing the standard uniform excitation.