OpenSees Cloud

OpenSees AMI

A Complicated Equivalent

Original Post - 01 May 2022 - Michael H. Scott

Visit Structural Analysis Is Simple on Substack.

Whether you use closed-form or numerical integration, the deflection at the free end of a laterally loaded linear-elastic, prismatic column is known to be PL³/(3EI). This result is easily verified in OpenSees with either an elasticBeamColumn element or a material nonlinear element with elastic sections.

Now suppose we philosophized a bit then posited the following modeling approach…

Instead of a single element for that column, let’s use a series of zero length rotational springs connected by flexurally rigid segments. The rotational springs are collocated with the integration points from whatever quadrature rule you like, e.g., three-point Gauss-Legendre or four-point Gauss-Lobatto as shown below, or any other integration option.

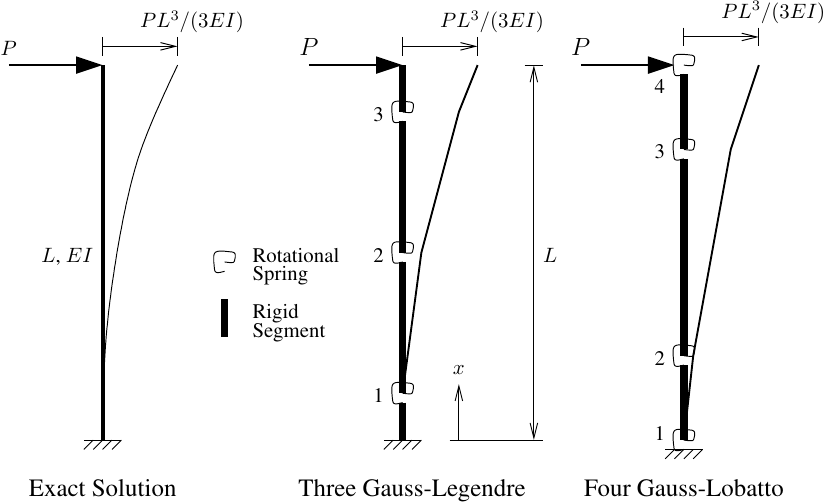
My question is, what stiffness should be assigned to each rotational spring in order to compute the correct free end deflection, PL³/(3EI), using a springs and rigid segments model?

1. EI
2. EI/L
3. 3EI/L
4. EI/w_i
5. EI*w_i
6. None of the above

In options D and E, w_i is the integration weight on the column domain [0,L] associated with quadrature point/spring location x_i, meaning the stiffness is not the same for each spring.

Post your answer with an explanation in the comments section below. I will explain the correct answer in a follow up post. Responses are due by May 31, 2022.

---

While you can develop a model in OpenSees or use good ‘ol pencil and paper to figure out the correct answer, I don’t recommend you use this modeling approach anywhere else. As usual, complicated is not better.

ANSWER