OpenSees Cloud

OpenSees AMI

A Rigid Bar Walks Into a Bar

Original Post - 02 Apr 2023 - Michael H. Scott

Visit Structural Analysis Is Simple on Substack.

OpenSees has two rigidLink commands that enforce constraints between a primary node (pNode) and a secondary node (sNode).

ops.rigidLink('-beam',pNode,sNode)
ops.rigidLink('-bar',pNode,sNode)

The beam option works well, enforcing linear kinematic constraints as if the two nodes were connected by a beam of infinite axial and flexural stiffness. The bar option should give constraints assuming only infinite axial stiffness.

But, like in Italy, the bar may not be what you think it is.

Consider the model shown below. Element 1 is an elasticBeamColumn element while element 2 is an elastic truss element.

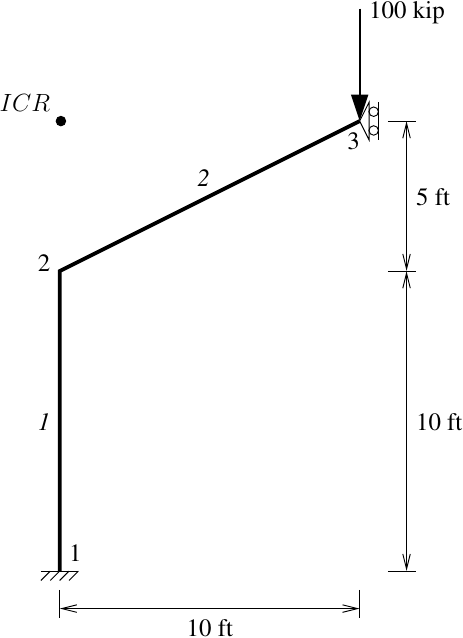
Due to a vertical load at node 3, with realistic member properties that give naturally high axial stiffness, element 2 will rotate about the instantaneous center of rotation (ICR) shown in the figure, and push element 1 to the left, as shown in the deformed shape below, plotted using opsvis.

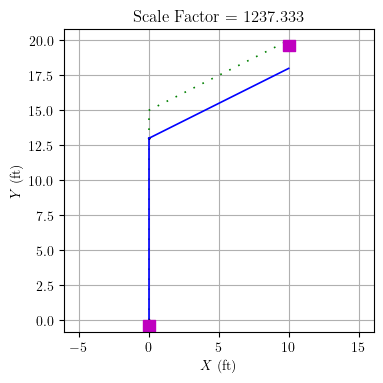
Now, let’s make the high axial stiffness of element 2 official by using a rigid link bar constraint. There should not be any significant difference in response because element 2 already has high axial stiffness.

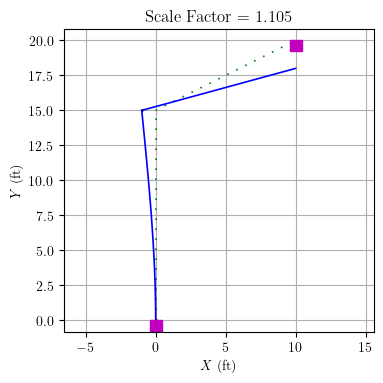
However, when we apply this constraint to the model, the deformed shape is totally different.

Now element 2 does not rotate, i.e., the ICR is at infinity. The vertical load transfers directly into axial compression of element 1. Note that the scale factor on the deformed shape is huge.

In addition, the support reactions of the model do not satisfy equilibrium. You have to include the “reactions” from node 2 in order to make global equilibrium work out.

So what’s the problem? No, we did not daisy chain the single point constraints at node 3 with the rigid link multi-point constraint.

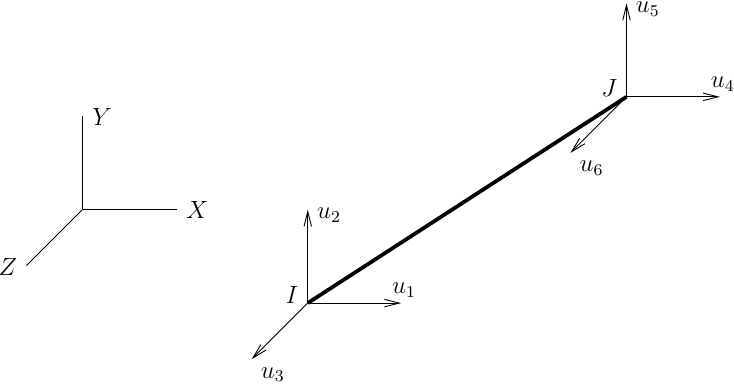
The problem is the rigid link bar in OpenSees constrains the translations at each node to be equal, i.e., the global X-displacements of the primary and secondary nodes are equal and the global Y-displacements of the primary and secondary nodes are also equal. Same thing for Z-displacements in 3D.

\(u_1=u_4\), \(u_2=u_5\), and \(u_3=u_6\)

The constraint equation for a rigid bar should be

where \(\Delta X=X_J-X_I\) is the difference in global X-coordinates of nodes I and J. Same for \(\Delta Y\) and \(\Delta Z\). From this constraint equation we can select one secondary DOF, e.g., u₁

Of course we have to check if \(\Delta X\) is zero. If so, we can rewrite the equation with u2 or u3 on the left-hand side.

But there’s really no easy way to pull off this constraint equation in OpenSees.

The MP_Constraint class, from which rigidLink, rigidDiaphragm, equalDOF, etc. are constructed, assumes the primary and secondary DOFs are at unique nodes. But with the rigid link bar option, the secondary DOF will be at the same node as one of the primary DOFs.

It’s possible to deal with this case by overloading the MP_Constraint constructor. But no one is beating down the bar doors for this functionality. Just be careful when using the rigid link bar command–in fact, I don’t recommend you use the command at all. The beam is fine, just not the bar.

And if you do want a stiff drink at an Italian bar, ask for a caffè corretto.