OpenSees Cloud
OpenSees AMI
Arc Length Parameters
Original Post - 02 May 2023 - Michael H. Scott
Visit Structural Analysis Is Simple on Substack.
Beyond load control, which cannot get past peaks in load-displacement response, OpenSees has several “continuation” methods for nonlinear static analysis of structural models.
Implementation of continuation methods is based on the incremental-iterative framework by Clarke and Hancock (1990) with displacement control, minimum unbalanced displacement norm (MUDN), and arc length among the most frequently used in OpenSees. Clarke and Hancock outline a few other strategies as well.
The gist of the incremental-iterative framework is the load factor, \(\lambda\), becomes a variable that is updated during equilibrium iteration with a load, or pseudo-time, step. The initial increment, \(\Delta\lambda^1\) is based on user input while the iterative updates, \(\Delta\lambda^{j+1}\), are computed based on a constraint equation.
Load control is a trivial incremental-iterative case with \(\Delta\lambda^1\) given by the user and the constraint \(\Delta\lambda^{j+1}=0\) enforced during equilibrium iteration.
The inputs for displacement control and MUDN are straightforward, but a frequent question is “what inputs should I used for arc length?”
Well, actually, there are two arc length integrators in
OpenSees–ArcLength and ArcLength1. Both versions take the arc length,
s, and an additional parameter, \(\alpha\).
ops.integrator('ArcLength',s,alpha)
ops.integrator('ArcLength1',s,alpha)
On the first equilibrium iteration within a load step, both arc length integrators compute the change in load factor, \(\Delta \lambda^1\), from the “tangent displacements”, \({\bf U}_{fT} = {\bf K}_T \backslash {\bf P}_{ref}\), and the user specified arc length and \(\alpha\).
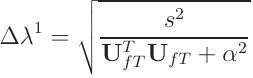
Because everything is squared, \(\Delta\lambda^1\) will always be
positive, which can be a problem if you are tracking post-peak response.
Both ArcLength and ArcLength1 will multiply \(\Delta\lambda^1\) by
the change in load factor from the previous step, i.e., if the load
factor decreased in the previous load step, the current load step will
start with a negative increment in load factor.
The \(\alpha\) parameter is important because the magnitude of the tangent displacements is usually very small for the common case where \({\bf P}_{ref}\) (your reference load pattern) contains unit values and \({\bf K}_T\) is close to the initial stiffness, i.e., in the early stages of loading or using Newton-Raphson with the initial stiffness on the first iteration. If you do use large reference loads, you’ll have to increase the input arc length.
When the magnitude of \({\bf U}_{fT}\) is small, using \(\alpha=1\) will make the initial change in load factor roughly equal to the input arc length, i.e., \(\Delta \lambda^1 \approx s\). If you set \(\alpha=0\), the initial change in load factor can be large, which is not such a bad thing when you’re trying to get through the first few steps of linear response during a pushover analysis.
Anyway, on subsequent iterations during a load step, you can let the arc
length integrators do their thing–ArcLength solves a quadratic
equation, while ArcLength1 solves a simplified equation, to get
\(\Delta \lambda^{j+1}\). I won’t go into other details, e.g., deciding
which root of the quadratic equation ArcLength uses.
The following guidelines will help you with the arc length integrators in OpenSees:
- Use small (unit) values in \({\bf P}_{ref}\)
- Set the arc length equal to the desired increment in load factor
- Use \(\alpha=1\) (default value) or \(\alpha=0\) if you feel bold
The two DOF spring system below demonstrates the arc length integrators in OpenSees for hardening response.
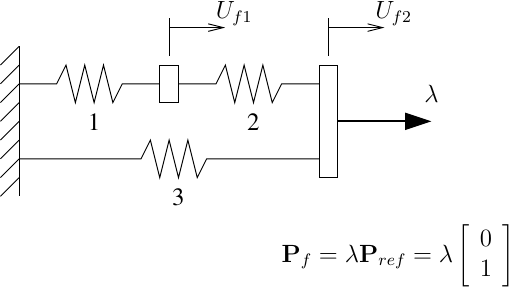
The force-deformation response of springs 1, 2, and 3 are \(p_b=10\arctan(u_b)\), \(p_b=4\arctan(0.5u_b)\), and \(p_b=7\arctan(u_b)\), respectively.
The response using 16 steps of load control with \(\Delta\lambda=1.0\) is compared with 16 steps of both arc length methods with arc length s=1.0 and \(\alpha\) equal to 1 and 0.
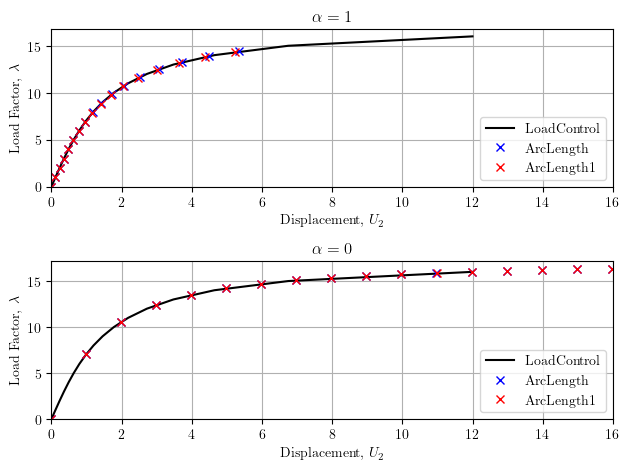
With \(\alpha=1\), the arc length integrators are on par with load
control as the system loses stiffness and ArcLength takes slightly
larger steps than ArcLength1. The arc length integrators give
essentially the same response when \(\alpha=0\), with both behaving
well as the system loses stiffness, where load control will fail if it
went on to step 17.
Note that \(\alpha=0\) is not somehow better than \(\alpha=1\). Just in this example, we didn’t take the \(\alpha=1\) case further on the load-displacement curve having limited the analysis to 16 steps. However, it is nice that the first few steps are larger when \(\alpha=0\).
More complex problems involving snap through and snap back will be the subject of other posts.