OpenSees Cloud

OpenSees AMI

One and Only One

Original Post - 18 Nov 2023 - Michael H. Scott

Visit Structural Analysis Is Simple on Substack.

Two element formulations in OpenSees–forceBeamColumnCBDI and mixedBeamColumn–are capable of handling geometric nonlinearity within the basic system, i.e., P-little-delta effects.

The CBDI formulation, described in Neuenhofer and Filippou (1998), approximates the transverse deflection using Lagrange polynomials fit through the curvature at each integration point. Due to the added computational expense and coding details, the forceBeamColumnCBDI element is a separate implementation from the well-known geometrically linear forceBeamColumn element.

The mixed formulation, summarized in Alemdar and White (2005), uses a shape function for the transverse deflection. With this relatively straightforward approach, the geometrically linear and nonlinear formulations are in the same mixedBeamColumn element with the -geomNonlinear input option.

Geometric nonlinearity inside the basic system means we should be able to capture critical flexural buckling loads using only one element per member. We can also use a corotational mesh of geometrically linear elements along the member length in order to capture geometric nonlinearity, but when it’s possible, a coarse mesh is preferred.

Consider a simple W10x54 column subject to flexure about its weak axis. Using a single geometrically nonlinear element, we should be able to capture flexural buckling. Small moments equal to 0.001EI/L are applied and held constant in order to induce first and second mode buckling under increasing axial load, P.

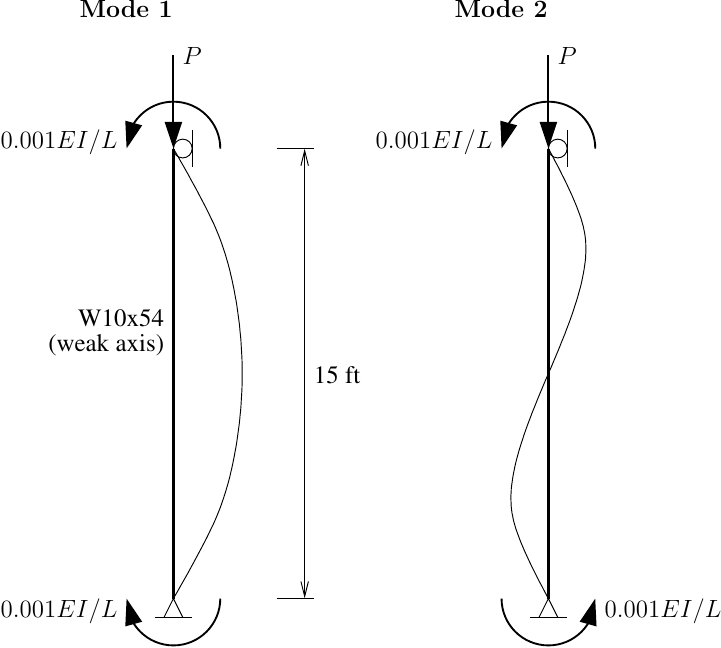
Each element formulation uses six Gauss-Legendre integration points. The CBDI formulation requires a decent number of integration points to capture the transverse deflection while the mixed formulation needs a minimum number of integration points in order to fully integrate the transverse deflection shape function in the element state determination.

The results for first mode buckling are shown below.

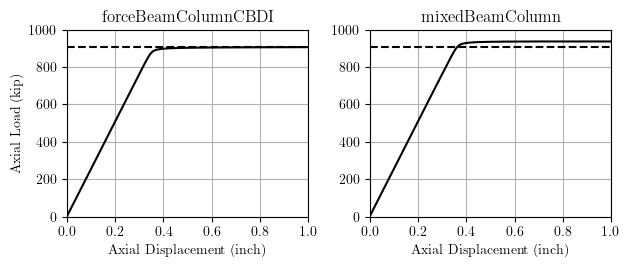
Both elements capture the first mode critical buckling load very well with forceBeamColumnCBDI a little under and mixedBeamColumn maybe a little over.

For the second mode, the mixed formulation over-predicts the buckling load by about 10%.

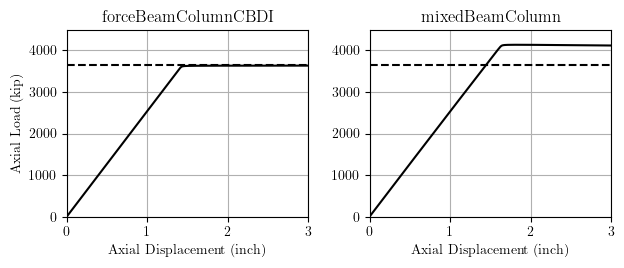
Both the forceBeamColumnCBDI and mixedBeamColumn geometrically nonlinear elements are also capable of handling material nonlinearity. The performance of a single element for inelastic buckling will be the subject of another post.