OpenSees Cloud

OpenSees AMI

Minimal Thermal Example

Original Post - 24 Jan 2024 - Michael H. Scott

Visit Structural Analysis Is Simple on Substack.

For verification purposes, I needed to come up with the fixed-end axial force for a beam subjected to uniform thermal expansion. It’s not rocket science, nowhere near an LPU, but a little pencil and paper and the free end axial deflection is \(\alpha (\Delta T) L\). The fixed-end axial force, to push the free end back to zero deflection, is then \(q_{b0}=EA\alpha(\Delta T)\).

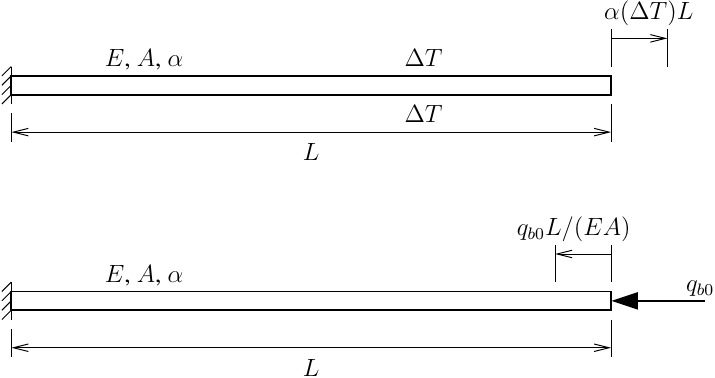
Naturally, I tried this verification using OpenSees thermal capabilities, which are somewhat hit and miss. Not unexpectedly, things got interesting.

There is no thermal truss element, so I used the forceBeamColumnThermal element, which basically mirrors the standard forceBeamColumn element. Nor is there a thermal elastic section, so I used FiberSectionThermal with the ElasticThermal uniaxial material, which I added to the OpenSeesPy interpreter after a small bug fix (PR #1337).

The thermal loading is defined using the -beamThermal option, which requires temperature to be specified at the bottom and top of the section. For uniform heating through the section, the temperatures are equal. The load pattern is defined with a linear time series as for nonlinear material response, you’ll want to ramp up the temperature.

In the script below, use any reasonable values for element length, L, rectangular cross-section dimensions, b and d, elastic modulus, E, coefficient of thermal expansion, alpha, and temperature change, deltaT.

import openseespy.opensees as ops

ops.wipe()
ops.model('basic','-ndm',2,'-ndf',3)

ops.node(1,0,0); ops.fix(1,1,1,1)
ops.node(2,L,0)

ops.uniaxialMaterial('ElasticThermal',1,E,alpha)

ops.section('FiberThermal',1)
ops.patch('rect',1,2,2,-d/2,-b/2,d/2,b/2)

ops.beamIntegration('Lobatto',1,1,3)

ops.geomTransf('Linear',1)
ops.element('forceBeamColumnThermal',1,1,2,1,1)

ops.timeSeries('Linear',1)
ops.pattern('Plain',1,1)
ops.eleLoad('-ele',1,'-type','-beamThermal',deltaT,-d/2,deltaT,d/2)

Nsteps = 1
ops.integrator('LoadControl',1/Nsteps)
ops.analysis('Static','-noWarnings')

ops.analyze(Nsteps)

With the forceBeamColumnThermal element, I obtained the expected free end axial deflection of \(\alpha (\Delta T) L\) using one time step. Same result when ramping the temperature up using 10 or 100 time steps.

But when I switched to dispBeamColumnThermal, the axial deflection changed based on the number of time steps, which should not happen because this analysis is linear. The results are shown below for increasing Nsteps in the script above.

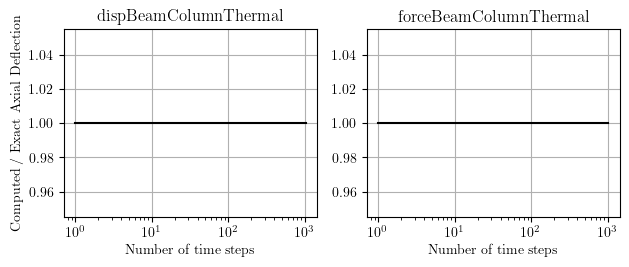
Clearly, there is a bug in the dispBeamColumnThermal element. Digging a little further, analysis with this element formulation leads to an axial reaction at the fixed end, which should not happen.

I’ll keep working with this minimal example to find the issue. Should be something simple, but probably not. If you have any additional information, please let me know!