Effective Earthquake Forces

Original Post - 02 Jun 2024 - Michael H. Scott

Visit Structural Analysis Is Simple on Substack.

There’s nothing special about the UniformExcitation load pattern in OpenSees. The pattern is a convenience for defining effective earthquake forces due to uniform ground acceleration as plain ‘ol mechanical loads on your model.

Consider the equation of motion for uniform ground acceleration, with linear inertia and damping forces, and influence vector \({\boldsymbol\iota}\) for the ground motion direction:

\[{\bf m}\ddot{\bf u} + {\bf c}\dot{\bf u} + {\bf p}({\bf u}) = -{\bf m}{\boldsymbol\iota}\ddot{u}_g(t)\]

The right-hand side forcing function is \({\bf p}_{eff}=-{\bf m}{\boldsymbol\iota}\ddot{u}_g(t)\), which is a product of reference loads \({\bf p}_{ref}=-{\bf m}{\boldsymbol\iota}\) and scalar time series \(\ddot{u}_g(t)\).

So, if you get an error using UniformExcitation, e.g., when attempting to apply vertical ground motion to a model that works perfectly fine for horizontal ground motion–or you just want to be sporty on any model–you can define effective earthquake forces yourself.

Inside a Plain pattern, loop over the nodes, get the nodal mass, then apply mass as reference load in the opposite direction.

dir = 1 # 1=X, 2=Y, 3=Z
ops.timeSeries('Path',1,'-dt',0.02,'-filePath','tabasFN.txt','-factor',386.4)
ops.pattern('Plain',1,1)
for nd in ops.getNodeTags():
    mass = ops.nodeMass(nd)
    ndf = len(mass)
    if dir > ndf or mass[dir-1] <= 0.0:
        continue
    peff = [0]*ndf
    peff[dir-1] = -mass[dir-1]
    ops.load(nd,*peff)

For a model with only nodal masses, the code snippet above is equivalent to using the following UniformExcitation pattern:

ops.timeSeries('Path',1,'-dt',0.02,'-filePath','tabasFN.txt','-factor',386.4)
ops.pattern('UniformExcitation',1,dir,'-accel',1)

A simple two-DOF model is shown below along with interpretations of the uniform excitation (UE) and effective force (EF) approaches.

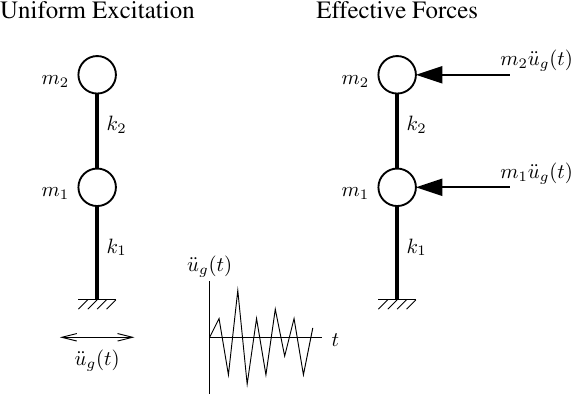
Two DOF model

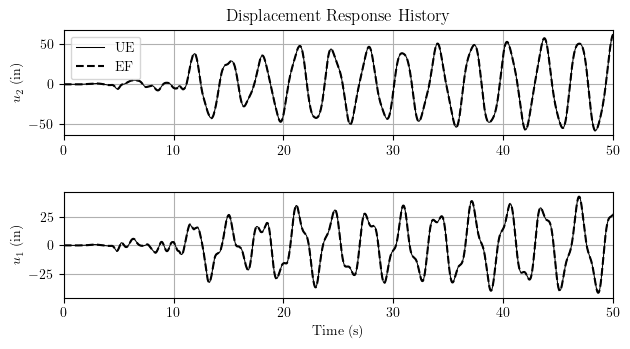
Applying the ground acceleration with the UniformExcitation pattern and with effective forces via the Plain load pattern (on a linear-elastic model with k₁=k₂=100 kip/in and m₁=m₂=10 kip-s²/in, and no damping) gives identical results.

Two DOF displacement response history

I’m not saying you should abandon the UniformExcitation pattern. Instead, I am pointing out that the pattern is a shortcut for defining earthquake forces. The do-it-yourself Plain load pattern approach can get messy with element mass, so stick with UniformExcitation.

OpenSees Cloud

OpenSees AMI

Effective Earthquake Forces