OpenSees Cloud

OpenSees AMI

Bring Your Own Matrix

Original Post - 27 Jul 2025 - Michael H. Scott

Visit Structural Analysis Is Simple on Substack.

Getting a stiffness matrix out of OpenSees is straightforward using printA(). But what about getting a stiffness matrix into OpenSees?

This is the situation I faced recently testing  BennySparse with linear systems from the  SuiteSparse Matrix Collection. I had no way of building an OpenSees model that could recreate those matrices.

After some trial and error, I found that regardless of how large the input matrix is, even if N is a million, you can construct the matrix in OpenSees from a 1D model with one fixed node and N free nodes.

import openseespy.opensees as ops
import numpy as np

ops.wipe()
ops.model('basic','-ndm',1,'-ndf',1)

ops.node(0,0); ops.fix(0,1)
for i in range(1,N+1):
   ops.node(i,0)

The N free nodes give a blank slate on which we can build the matrix using zero length elements. Two cases must be examined.

Diagonal Entries

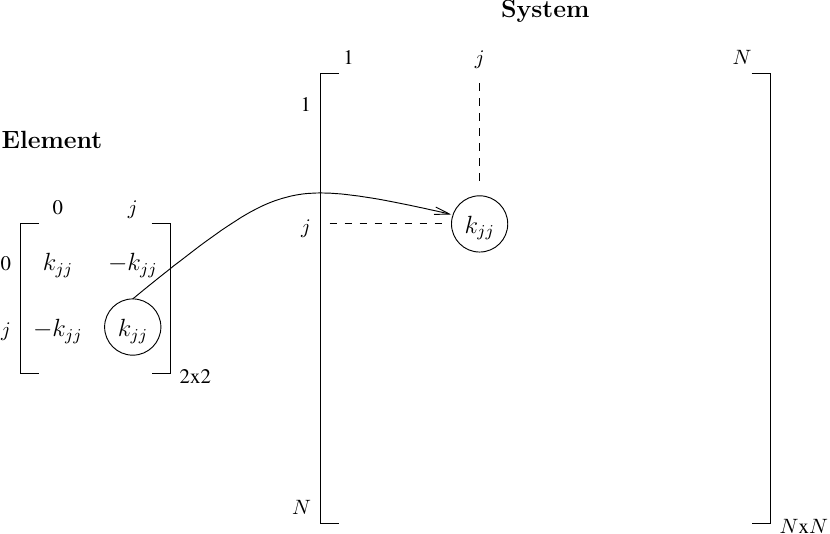
For matrix entries, k_jj, on the diagonal, we connect a zero length element from base node 0 to node j.

ops.uniaxialMaterial('Elastic',23,kjj)
ops.element('zeroLength',23,0,j,'-mat',23,'-dir',1)

This 1D zero length element gives the 2x2 stiffness matrix shown below. Because one of the element nodes is fixed (node 0), only the diagonal entry corresponding to node j will be assembled onto the diagonal of the system stiffness matrix.

Off-Diagonal Entries

For off-diagonal matrix entries, connecting a zero length element of stiffness k_ij between nodes i and j will have the wrong sign on the off-diagonal terms and will lead to additional stiffness on the diagonal at equations i and j.

To make things right in the assembled stiffness matrix, we have to flip the sign on the element stiffness and use two more zero length elements so that the added stiffness is zero on the diagonal.

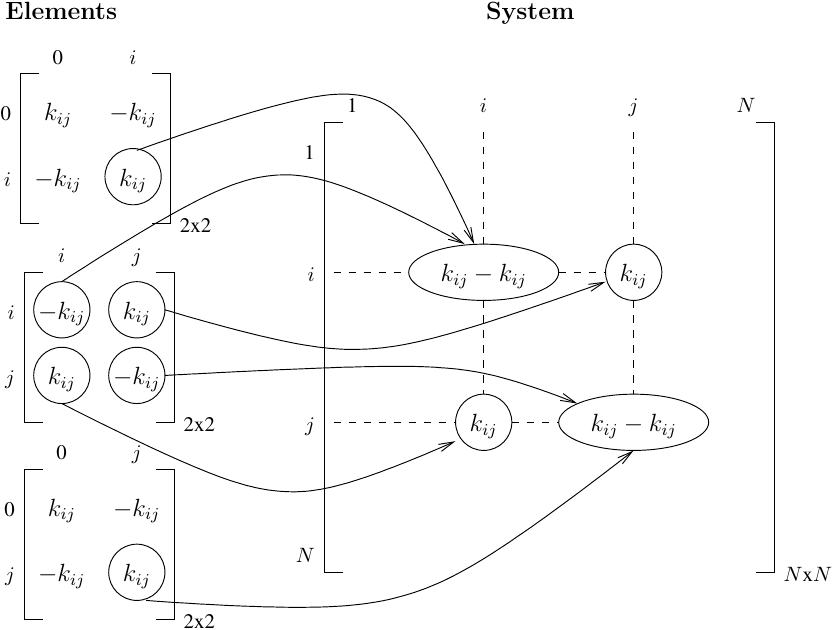
The definition of the three zero length elements is shown below. Note that the material for the element connecting nodes i and j has negative k_ij as its stiffness.

ops.uniaxialMaterial('Elastic',24,-kij)
ops.element('zeroLength',24,i,j,'-mat',24,'-dir',1)

ops.uniaxialMaterial('Elastic',25,kij)
ops.element('zeroLength',25,0,i,'-mat',25,'-dir',1)
ops.element('zeroLength',26,0,j,'-mat',26,'-dir',1)

This approach works for bringing in symmetric matrices. For non-symmetric matrices, instead of three zero length elements, you can use one linearElasticSpring element to handle the off-diagonal entries. The linearElasticSpring element should work for symmetric matrices too.

Minimal Example

Suppose we want to bring the following symmetric matrix into OpenSees.

Although this matrix is too small to fuss over sparsity, let’s assume the lower triangle of the matrix is stored as (row,col,value) triplets, a common format for sparse matrices.

triplets = [(1,1,4),(3,1,2),(2,2,1),(3,3,4)]

You can store matrices in other formats, e.g., all the entries, in a file, etc. No importa.

The code below loops over the triplets to form the user-supplied matrix. Anything above the diagonal (if present) is ignored via the  if i < j: conditional so that we don’t double count off-diagonal entries. We also ignore any matrix entries with zero value.

matTag = 0
eleTag = 0
for i,j,kij in triplets:
   if abs(kij) == 0.0 or i < j: # Ignore zeros and upper triangle if present
      continue
   matTag += 1
   ops.uniaxialMaterial('Elastic',matTag,kij)
   if i == j:
      eleTag += 1
      ops.element('zeroLength',eleTag,0,j,'-mat',matTag,'-dir',1)
   else:
      ops.uniaxialMaterial('Elastic',-matTag,-kij)
      eleTag += 1
      ops.element('zeroLength',eleTag,i,j,'-mat',-matTag,'-dir',1)
      eleTag += 1
      ops.element('zeroLength',eleTag,0,i,'-mat', matTag,'-dir',1)
      eleTag += 1
      ops.element('zeroLength',eleTag,0,j,'-mat', matTag,'-dir',1)

ops.numberer('Plain')
ops.system('FullGeneral')
ops.analysis('Static','-noWarnings')
ops.analyze(1)

K = np.array(ops.printA('-ret')).reshape((N,N))
assert (K == [[4,0,2],[0,1,0],[2,0,4]]).all()

The solver above is FullGeneral and the numberer is Plain so we can use printA on the assembled, un-permuted matrix and perform an assertion. But if you want to supply pairs of time series/load patterns and solve for displacements against the assembled matrix, you can use whatever system and numberer you like.

This approach to inputting a stiffness matrix can create a lot of zero length elements (one for every diagonal entry and three for every off-diagonal) and can incur significant memory overhead, i.e., you could run out of RAM for large matrices. Also, due to the large number of elements, assembling the matrix can take a while for large systems. I could write a specialized 1D BYOM element, but not much of a win there unless turning OpenSees into some weird form of MATLAB is a feature users want.

What About Mass and Damping?

OpenSees does not store separate mass, damping, and stiffness matrices, but you can bring your own mass matrix to an OpenSees model with 1D inerter elements, or nodal masses if the mass matrix you’re bringing is diagonal. And you can bring your own damping matrix using zero length elements with viscous elastic materials. Bringing your own mass and damping could be a post for another day.

To test the solvers available in OpenSees on large sparse matrices, take a look at the  ssgetpy  Python package which searches and downloads matrices from the  SuiteSparse Matrix Collection.